Алгоритм производит разбиение произвольного(в смысле выпуклости) многоугольника на треугольники.

Пусть некоторый многоугольник задан набором координат своих вершин P0=(x0,y0);P1=(x1,y1);...;Pn=(xn,yn) 
при этом будем полагать, что вершины занумерованы по часовой стрелке. В случае если многоугольник 
выпуклый, задача нахождения разбиения тривиальна, можно взять набор диагоналей выходящих из какой-либо 
вершины. 



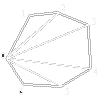В случае невыпуклого многоугольника задача существенно усложняется. Будем действовать следующим образом, 
на каждом шаге алгоритма будем отсекать один треугольник Pi-1,Pi,Pi+1 и исключать вершину Pi из 
дальнейшего рассмотрения. Чтобы определить можно ли использовать диагональ Pi-1Pi+1 для отсечения 
треугольника, будем вначале проверять знак sin угла Pi-1,Pi,Pi+1 учитывая при этом последовательность 
обхода вершин, так для многоугольника изображенного на рисунке при i=0,1,2,3,4,7 sin будет отрицателен, 
а при i=5,6 положителен. 



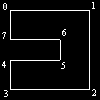Далее найдя i для которой sin отрицателен, проверем не входят ли в треугольник Pi-1,Pi,Pi+1, какие-либо 
точки из многоугольника (естественно кроме i-1,i,i+1), если нет значит отсечем этот треугольник, иначе 
ищем следующую вершину с отрицательным sin и проверяем ее. Проверку принадлежности точки треугольнику 
можно осуществить одним из алгоритмов рассмотренных на этой странице переписав его для частного случае 
треугольника. 
Алгоритм можно оптимизировать по скорости введя, например массив, содержащий знаки sin, и перевычисляя на 
каждом шаге только i - й знак. Возможны и другие усовершенствования. 
Теперь немного о блок-схеме реализующей алгоритм. Номер последней вершины передается в переменной n 
(всего будет соответственно n+1 вершина), координаты в массивах x и y, полученое разбиение помещается в 
массив tr, tr[1..3][i] содержит номера вершин исходного многоугольника, составляющие i-ый треугольник. 
Внутри блок-схемы дополнительно используются массив t для хранения вершин промежуточных многоугольников.